مثال ۱.۰۲: هندل کردن داده های ناجور
مثال ۱.۰۲: سر و کلّهزدن با دادههای بهمریخته
در این مثال، ما با دیتاست tips که قبلا برای اولین بار در مثال 1.01 با آن برخورد داشتیم به عنوان نمونهای بمنظور نشاندادن نحوهی برخورد با دادههای بهمریخته استفاده خواهیمکرد. برای تکمیل این مثال، مراحل زیر را دنبال کنید:
1) در ابتدا یک نوتبوک Jupyter بمنظور پیادهسازی این مثال باز کنید.
2) اول تمام موارد موردنیاز را فراخوانیکنید، سپس دیتاست tips را بارگذاری کرده و آن را در متغیری به نام: " tips " ذخیره کنید:
Jupyter Notebook
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
tips = sns.load_dataset('tips')
tips
دیتاست موردنظر بشکل زیر خواهد بود: (به فیچرها توجه داشته باشید.)
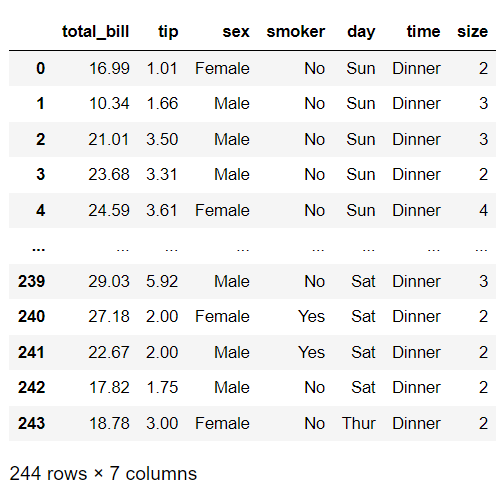
3) در قدم بعد یک متغیر به نام: " size " ایجاد کنید تا مقادیر فیچر متناظر با آنرا ذخیره کنید. از آنجایی که این دیتاست حاوی دادهی ناموجود یا گمشدهای(missing data) نیست، در راستای اهداف آموزشی این مثال، 16 مقدار اول متغیر size را به مقادیر گمشده (missing data) تبدیل می کنیم؛ سپس 20 مقدار اولیه را هم چاپ میکنیم تا از انجام این امر مطمئن شویم:
Jupyter Notebook
size = tips["size"]
size.loc[:15] = np.nan
size.head(20)
توجه داشته باشید که ممکن است در این مرحله یک هشدار محتوی این پیام ظاهر شود: " A value is trying to be set on a copy of a slice from a DataFrame " ؛ علت این اتفاق به آنجائی برمیگردد که خودِ size بخشی از دیتاست tips میباشد و طبیعتا با ایجاد تغییر در آن، دیتاست هم تغییر میکند. این قضیه اصلا مشکلی ندارد زیرا هدف ما در این مثال ویرایش مقادیر فیچرهای دیتاست و سپس اصلاح دیتاست میباشد.
با روشن شدن علت این قضیه به شرح خود کد برمیگردیم. در این قطعه کد، ما متغیری به نام: "size " ایجاد کردیم که در واقع بخشی از دیتاست میباشد و سپس 16 مقدار اول آنرا به: " NaN " مخفف: " Not a Number " تغییر دادیم که در واقع نشاندهندهی مقادیر ناموجود یا گمشده(missing value) میباشد. در خط آخر هم 20 مقدار اول را چاپ کردیم.
خروجی بصورت زیر خواهد بود:

همانطور که مشاهده میکنید فیچر موردنظر ما الان شامل یکسری مقادیر NaN هست.
4) ابعاد متغیر size را به شکل زیر چک کنید:
Jupyter Notebook
size.shapeخروجی به صورت زیر خواهد بود:
(244,)
5) اکنون از این بین، تعداد مقادیر NaN را میشماریم تا ببینیم که چگونه باید باید با آنها سر و کله بزنیم. بدین منظور از تابع: " ()isnull " برای یافتن مقادیر NaN و تابع: " ()sum " برای جمع کردنشان استفاده میکنیم:
Jupyter Notebook
size.isnull().sum()
خروجی به صورت زیر خواهد بود:
Jupyter Notebook
16
از بین کل مقادیر متغیر size، فقط 6.55 درصد از آنها NaN میباشند(100 * 16/244). مسلما این درصد آنقدری بزرگ نیست که بخواهیم کل فیچر را حذف کنیم،اما با این وجود باز هم نیاز داریم تا این مقادیر را به نحوی هندل کنیم.
6) بدین منظور از روش انتساب میانگین برای جایگزینکردن مقادیر از ناموجود یا گمشده(missing values) استفاده میکنیم. برای انجام این کار، ابتدا باید میانگین مقادیر موجود را محاسبه کنیم:
Jupyter Notebook
mean = size.mean()
mean = round(mean)
print(mean)
خروجی حاصل مساوی 3 میشود.
نکتهای که باید در اینجا به آن توجه کنید این است که مقدار میانگین (2.55) به نزدیکترین عدد صحیح گرد شده است، زیرا فیچر موردنظر ما یا همان size درواقع نشاندهندهی تعداد افرادی است که به گارسون انعام دادهاند.
7) در قدم بعدی، قصد داریم که تمام مقادیر ناموجود را با میانگین بدستآمده از مرحلهی قبل جایگزین کنیم. بدین منظور از تابع: " ()fillna " استفاده میکنیم؛ کاری که این تابع میکند این است که سراغ تکبهتک مقادیر NaN رفته و آنها را با مقدار تعریف شدهی داخل پرانتز(mean) جایگزین میکند. نهایتا برای بررسی اینکه آیا مقادیر موردنظر بدرستی جایگزین شدهاند یا نه، 20 مقدار اول را دوباره چاپ میکنیم:
Jupyter Notebook
size.fillna(mean, inplace=True)
size.head(20)نکتهای که باید به آن توجه کنید این است که وفتی پارامترِ inplace روی True تنظیم شده باشد، دیتاست اصلی ویرایش میشود؛ در غیر اینصورت فقط میتوان یک کپی از آن ایجاد و در متغیری جدید ذخیره کرد تا دیتاست اصلی دست نخورده باقی بماند.
خروجی چاپ شده به صورت زیر خواهد بود:
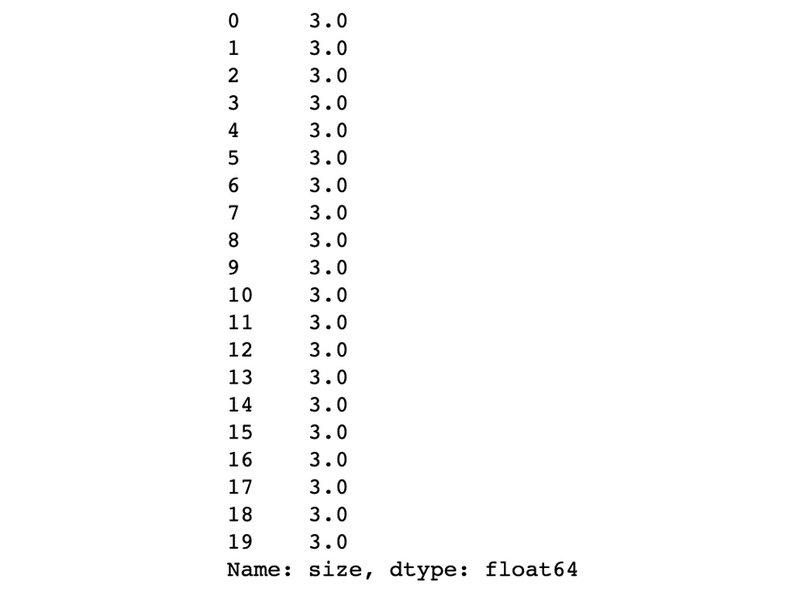
همانطوریکه در تصویر بالا مشاهده میکنید، مقادیر متناظر با NaN به 3 تغییر کردهاند، که در واقع همان میانگینی است که قبلا محاسبه کردیم.
8) به کمک کتابخانهی Matplotlib ، یک نمودار ستونی یا هیستوگرام(histogram) را بر اساس مقادیر متغیر size ترسیم میکنیم. بدین منظور مطابق کد زیر از تابع: " ()hist " استفاده میکنیم:
Jupyter Notebook
plt.hist(size)
plt.show()
هیستوگرام ترسیم شده بصورت زیر خواهد بود که اگر توجه کنید، مشابه فرم کلّیِ توزیع گاوسی میباشد:
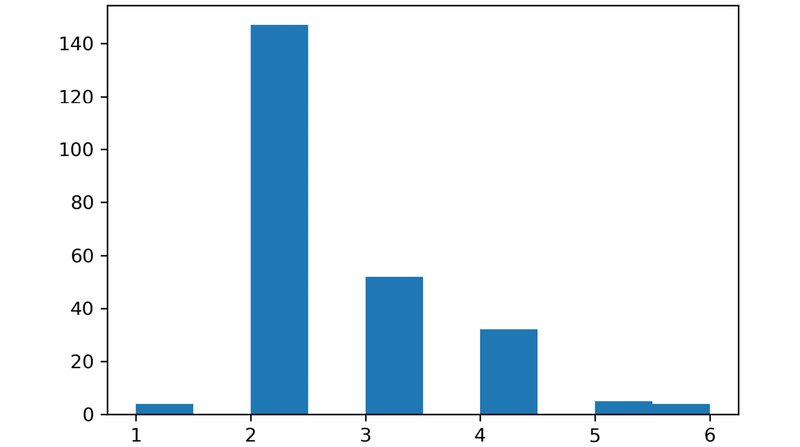
9) در این مرحله قصد داریم که نقاط پرت یا به اصطلاح Outlier ها را پیدا کنیم. بدین منظور از سه برابرِ انحراف معیار به عنوان مقیاسی برای محاسبهی مقادیر مینیموم و ماکسیموم استفاده میکنیم.
همانطور که قبلاً صحبت کردیم، مقدار مینیموم از حاصل تفریق مقدار میانگین از 3 برابرِ انحراف معیار بدست میآید. به همین دلیل طبق قطعه کد زیر جلو رفته و مقدار مینیموم را محاسبه کرده و داخل متغیری به نام: " min_val " ذخیره میکنیم:
Jupyter Notebook
min_val = size.mean() - (3 * size.std())
print(min_val)
مقدار مینیموم حدودا برابر: " 0.1974- " میشود که با توجه به آن میتوان چنین نتیجه گرفت که هیچ نقطهی پرتی(Outlier) در انتهای چپ توزیع گاوسی وجود ندارد.
نقطه مقابل مقدار مینیموم، ماکسیموم میباشد که طبیعتا از حاصلجمع مقدار میانگین با 3 برابرِ انحراف معیار بدست میآید. مطابق کد زیر، ماکسیموم را محاسبه کرده و داخل متغیری به نام: " max_val " ذخیره میکنیم:
Jupyter Notebook
max_val = size.mean() + (3 * size.std())
print(max_val)
مشاهده خواهید کرد که ماکسیموم حدودا 5.3695 درآمده و نشان از این دارد که نمونه دادههای بالاتر از 5.36 در حکم نقاط پرت یا Outlier ها میباشند که اگر به نمودار توجه کنید متوجه میشوید که ما در انتهای سمت راست توزیع گاوسی، یکسری نقاط پرت داریم.
10) حالا برای اینکه برخورد مناسبی با این نقاط پرت داشته باشیم، باید ابتدا از تعداد آنها مطلع شویم. بدین منظور به کمک indexing، تمامی مقادیری که داخل متغیر size قرار داشته و از ماکسیمومی که پیدا کرده ایم بزرگتر میباشند را پیدا کرده و داخل یک متغیر جدید به نام: " Outliers " میریزیم و نهایتا هم تعداد آنها را میشماریم:
Jupyter Notebook
outliers = size[size > max_val]
outliers.count()
خروجی بدست آمده نشان از آن خواهد داشت که 4 نقطهی پرت یا Outlier وجود دارد.
11) نقاط پرت را چاپ میکنیم تا مطمئن شویم که طبق منطق ماجرا، مقادیر صحیحی را ذخیره کردیم:
Jupyter Notebook
print(outliers)
خروجی به صورت زیر خواهدبود:
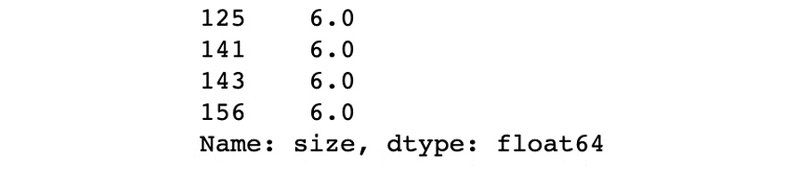
از آنجائیکه تعداد نقاط پرت کم بوده و به احتمال قوی مقادیرشان واقعی است یا به اصطلاح: " True Outlier " هستند، میتوانیم حذفشان کنیم.
نکته:
در این مثال، نمونههای متناظر با مقادیر پرتِ حاضر در متغیر size را حذف میکنیم تا صرفا با روند هندل کردن نقاط پرت آشنا شویم. گرچه در مثال های آینده، حذف کردن نقاط پرت با عنایت به تمام فیچرها انجام خواهد شد تا در صورت نیاز همهی نمونههای ثبت شده را حذف کنیم و نه فقط آنهایی را که برای فیچرِ size ثبت شدهاند.
12) دوباره به کمک indexing، مقادیر ذخیره شده در متغیر size را دوباره تعریف میکنیم تا فقط مقادیری که کوچکتر از حد ماکسیموم هستند را شامل شود. نهایتا هم ابعاد متغیر را دوباره چاپ میکنیم تا از حذف شدن نقاط پرت مطمئن شویم:
Jupyter Notebook
size = size[size <= max_val]
size.shape
خروجی به صورت زیر خواهد بود:
Jupyter Notebook
(240,)
همانطور که میبینید، ابعاد متغیر size که قبلا نیز در مرحله 4 محاسبه شده بود، 4 واحد کاهش یافته است که در واقع به تعداد نقاط پرت یا همان Outlier های ما میباشد.
مثال ما هم در این مرحله به پایان میرسد!
جمع بندی
ما قبلا اهمیت پیشپردازش دادهها را مورد بحث قرار داده و دیدیم که عدم انجام این کار ممکن است منجر به بایاس شدن مدل شده و بر زمان آموزش مدل و عملکرد آن تأثیر بگذارد. چالش اصلی ما در فاز پیشپردازش دادهها نیز به نحوهی هندلکردن دادههای نامرتب(messy data) مربوط است که برخی از اصلیترین فرمهای آن عبارتند از: مقادیر ناموجود یا گمشده(missing values)، نقاط پرت(outliers) و دادههای نویزدار.
همانطوریکه از اسم مقادیر ناموجود یا missing values پیداست، مقادیری هستند که خالی یا تهی یا به اصطلاح null میباشند. هنگام برخورد با تعداد زیادی missing values ، یا باید آنها را حذف کنید یا مقادیر جدیدی به آنها اختصاص دهید که در ادامهی دوره بطور مفصل به معرفی دو روشی که بمنظور اختصاص مقادیر جدید بکار میروند خواهیم پرداخت که این دو روش عبارتند از: انتستاب میانگین و رگرسیون.
نقاط پرت یا Outliers هم به مقادیری گفته میشود که از میانگین مقادیر یک فیچر فاصله زیادی دارند. یکی از راههای تشخیص Outlier ها به کمک انحراف معیار میباشد که در این مثال بررسی شد. نقاط پرت یا Outlier ها دو دسته هستند: False Values یا مقادیری که به اشتباه ثبت شدهاند و عملا وجود آنها با توجه به کلیات دیتاست غیرممکن است(مثل حالتی که در دیتاستِ حقوق کارمندان یک شرکت، یک کارمند نوپا وجود داشته باشد که حقوقی معادل حقوق یک رئیس را دریافت کند!)؛ True Values یا مقادیر واقعی و صحیحی که وجود آنها ممکن است اما سِنخیتی با دادههای هم صنف خود ندارند(مثل حالتی که دادههای مربوط به رئیس یک شرکت در بین دیتاست کارمندان قرار گیرد). این دو دسته باید به روش های متفاوتی هندل شوند، بدین صورت که True Outlier ها یا باید کلا حذف شوند یا با یک کران بالا تقریب زده شوند اما False Values باید با یک مقدار مناسب جایگزین شوند.
نهایتا هم دادههای نویزدار یا noisy data را داریم که صرف نظر از فاصله آنها با میانگین کل مقادیر، حاصل یکسری اشتباهات ناخواسته و اشتباهات تایپی باشند. این دادهها میتوانند عددی(numerical)، نامی(nominal) یا ترتیبی(ordinal) باشند.
نکته:
همواره به یاد داشته باشید که دادههای عددی همیشه با اعداد مقیاسدار یا قابل اندازهگیری نشان داده میشوند، دادههای نامی به آن دسته از دادههای متنی اشاره میکنند که از هیچ ترتیبی پیروی نمیکنند، و دادههای ترتیبی نیز به آن دسته از دادههای متنی اشاره دارند که از یک ترتیب معین پیروی میکنند.
