پیچیدگی زمانی

تا به اینجا در این کارگاه کدهایی که نوشتیم و بررسی کردیم تقریبا در کثری از ثانیه اجرا می شدند. کامپیوترهای مدرن(از سال 2005 به بعد) بسیار سریع هستند و تفاوت 10 تکرار یا 1000 تکرار حلقه توسط آنها برای ما بسیار کند به نظر می رسد. البته الگوریتم های مختلف نیز در سرعت اجرا تاثیر دارند و در اکثر مواقع زمانی که داده ها و مسئله بزرگ می شود، آنها نیز کارایی خود را از دست می دهند. به مسئله ی کاهش کارایی با افزایش ابعاد ورودی پیچیدگی( complexity ) گفته می شود.

در این کارگاه دوبار مسئله ی پیچیدگی را بررسی می کنیم. یک بار در همین فصل به صورت ساده و کاربردی و بار دیگر در فصل 13 ام با هدف آشنایی شما با مفهوم دقیق پیچیدگی و طراحی ساختارهای بهینه

در اندازه گیری پیچیدگی هدف ما این است که بدانیم با تغییر ابعاد مسئله چقدر زمان طول می کشد تا یک الگوریتم اجرا شود؟ اگر مسئله 10 برابر بزرگ شود( مثلا 1,000 بار اجرای حلقه به 10,000 بار تبدیل شود) آیا الگوریتم به 10 برابر زمان برای اجرا نیاز دارد؟ یا 100 برابر؟ یا تنها 2 برابر؟ یا اصلا ابعاد ورودی مسئله در سرعت اجرا تاثیری ندارد؟

این رابطه ی مستقیم بین اندازه مسئله و سرعت و تعداد مراحل اجرای الگوریتم را پیچیدگی زمانی( time complexity ) می نامیم.

درست است که میشود به سادگی زمان اجرای یک الگوریتم را روی مسائل با ابعاد ابعاد مختلف اندازه گیری و مشاهده کرد و نمودار افزایش سایز مسئله به سرعت اجرای آنرا رسم نمود و برای الگوریتم های پیچیده از این راه استفاده می شود؛ اما راه بهتری برای بررسی time complexity بیشتر الگوریتم ها وجود دارد که ارتباط بین سرعت و ابعاد را به صورت تئوری مشخص می کند. البته فاکتورهای مهم دیگری نیز در دنیای واقعی وجود دارد که میتواند سرعت اجرای برنامه را دچار اختلال کنند مثلا اینکه حافظه ی کافی در دسترس الگوریتم هست یا نه، نوع و سرعت پردازنده، فضای دیسک و دیگر پردازش هایی( processes ) که منابع ماشین را درگیر می کنند.

برای ساده سازی مسئله ی time complexity و در نظر نگرفتن موارد پیچیده، ما تنها تعداد عملیاتی را شمارش می کنیم که باید انجام شوند تا الگوریتم به پایان برسد. نتیجه ی این شمارش را با مفهوم O(اُ بزرگ) یا big-O (یا big-O notation ) نمایش می دهیم.

مثلا (n)O به این معناست که برای مسئله ای با سایز(size) n، تعداد n مرحله(step) طول می کشد تا الگوریتم اجرا شود و سرعت اجرا با n رابطه مستقیم دارد. در واقع سرعت اجرای برنامه به صورت زیر خواهد بود:

در فرمول بالا آلفا و بتا اعداد ثابتی هستند. آلفا زمان اجرای هر مرحله را مشخص می کند و بتا نیز جمع زمان ابتدا و انتهایی اجرای برنامه است که در یک مرحله اجرا می شوند. مثلا در مثال قبل زمان لازم برای تعریف لیست، متغیر ماکزیمم (ابتدای برنامه) و نمایش ماکزیمم(انتهای برنامه) را بتا در نظر میگیریم و زمان اجرای هر تکرار حلقه را آلفا.

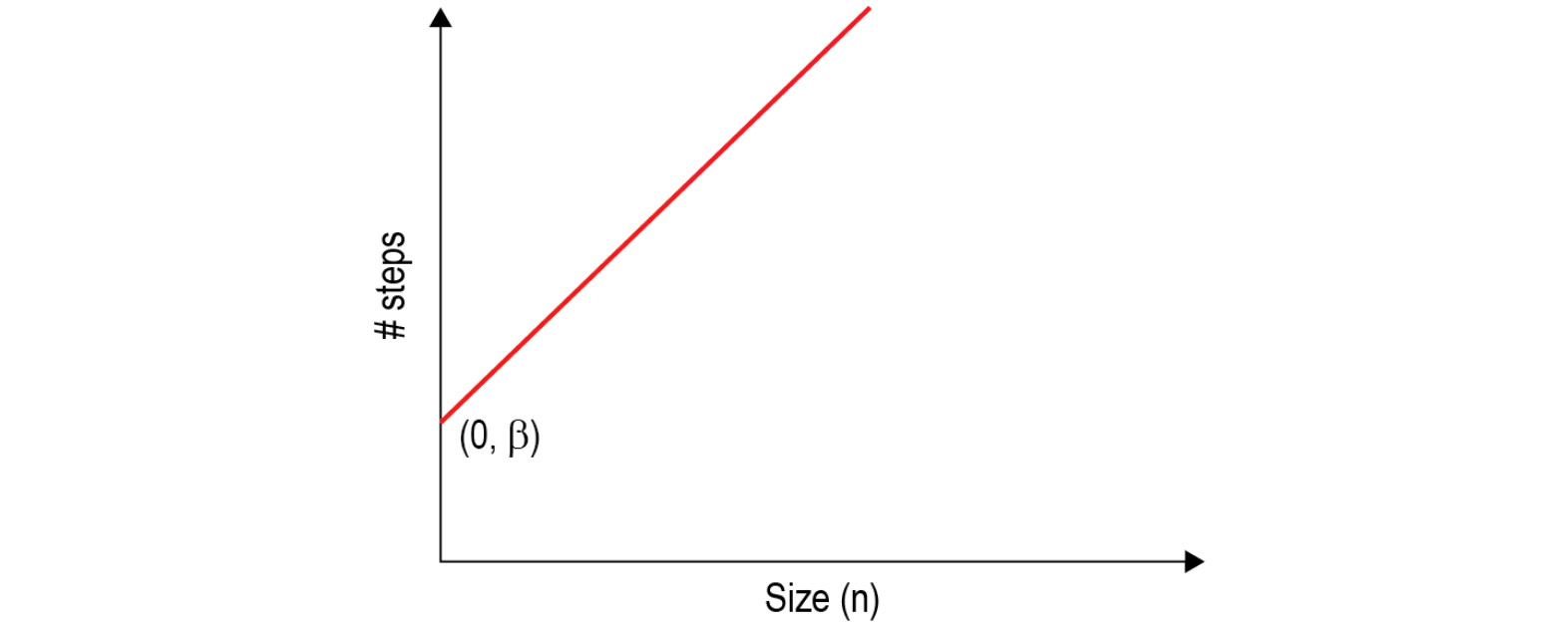
به حالتی که در بالا بررسی کرده ایم حالت زمان خطی ( Linear time ) گفته می شود و آنرا با (n)O نمایش می دهیم.

حالت های دیگری نیز وجود دارند که معروف ترین آنها به شرح زیر است:

زمان ثابت( Constant time ) : در این حالت زمان همیشه مقدار ثابتی خواهد بود و با افزایش سایز مسئله سرعت اجرای برنامه ثابت می ماند، مثلا زمانی که با استفاده از index میخواهیم به داده ی یک لیست دسترسی داشته باشیم. موارد مختلف دیگری را نیز در فصل 13 یاد خواهید گرفت. این حالت را با نشان (1)O می دهند.

زمان مربعی( Quadratic time ): در این حالت زمان اجرای برنامه با مربع سایز مسئله مرتبط است، مثلا در الگوریتم مرتب سازی حبابی (مثال 39). این حالت را با (n^2)O نشان می دهند.

زمان لگاریتمی( Logarithmic time ): در این حالت سرعت اجرای برنامه با لگاریتم سایز مسئله متناسب است، مثلا در الگوریتم جستجوی باینری (مثال 41). این حالت را با (Log n)O نشان می دهند.